Theory of Elasticity / Advanced Solid Mechanics
Abdul Azeem
8:34:43
Description
elasticity, solid mechanics, stress analysis
What You'll Learn?
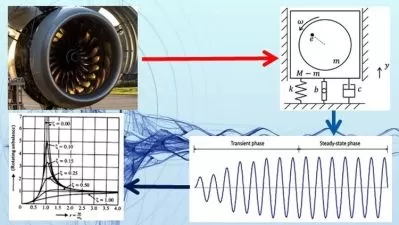
- Define and use the notation for forces and stresses in different directions and planes
- Identify and calculate the principal stresses, principal planes, stress invariants, mean and deviator stress, strain energy and distortion strain energy
- Solve two-dimensional problems in Cartesian co-ordinates using polynomials, St. Venant’s principle, uniqueness of solution, and Airy’s stress function
- Solve two-dimensional problems in polar co-ordinates using the stress-strain components, equilibrium and compatibility equations, and Airy’s stress function
- Solve torsion problems for bars with different shapes and cross-sections using the stress function method, energy method, soap films, and membrane analogy
Who is this for?
What You Need to Know?
More details
DescriptionThis course introduces the basic concepts and methods of elasticity theory, which is the study of how materials deform and stress under external forces. The course objectives are to enable the students to:
Understand the definitions and notations of forces, stresses, strains, and Hooke’s law in two and three dimensions.
Apply the transformation of stress and strain components under different coordinate systems.
Identify the principal stresses and strains, stress and strain invariants, strain energy, and superposition principle.
Solve two-dimensional problems in Cartesian and polar coordinates using Airy’s stress function method.
Analyze torsion of bars with different cross-sectional shapes using stress function, energy, and numerical methods.
The course will also expose the students to some experimental techniques and analytical tools for solving elasticity problems, such as soap films and Prandtl’s membrane analogy. The course will require the students to apply the concepts and methods learned in class to solve homework assignments and design projects. The course will also prepare the students for more advanced courses in solid mechanics, such as plasticity, fracture mechanics, and finite element analysis. The course is suitable for students who have completed courses in engineering mechanics, mathematics, and physics. The course will be taught through online video lectures.
The topics covered in this course are:
Introduction: Definition and notation for forces and stresses, components of stress and strain, Generalized Hooke’s law, Stress-strain relations in three directions, Plane stress and plane strain, Equations of equilibrium and compatibility in two and three dimensions, Stress components on an oblique plane, Transformation of stress components under change of co-ordinate system.
Principal stresses and principal planes: Stress invariants, Mean and Deviator stress, Strain energy per unit volume, Distortion strain energy per unit volume, Octahedral shear stress, Strain of a line element. Principal strains, Strain invariants, Volume strain, Principle of superposition, reciprocal theorem.
Two dimensional problems in Cartesian co-ordinates: Solution by polynomials, St. Venant’s Principle, Uniqueness of solution, Stress components in terms of Airy’s stress function. Applications to Cantilever, simply supported and fixed beams with simple loading.
Two dimensional problems in Polar co-ordinates: Stress-strain components, Equilibrium equations, Compatibility equations, Applications using Airy’s strain functions in polar co-ordinates for stress distributions symmetric about an axis, Effect of hole on stress distribution in a plate in tension, Stress due to load at a point on a semi-infinite straight boundary, Stresses in a circular disc under diametrical loading.
Torsion: Torsion of various shapes of bars, Stress function method of solution applied to circular and elliptical bars, Torsion of rectangular bars, Solution of Torsional problems by energy method, use of soap films in solving torsion problems, Prandtl’s membrane analogy. Solution of torsion of rectangular bars by (i) Raleigh Ritz method and (ii) Finite difference method.
Who this course is for:
- This course is intended for ME or MTech Structural Engineering students
This course introduces the basic concepts and methods of elasticity theory, which is the study of how materials deform and stress under external forces. The course objectives are to enable the students to:
Understand the definitions and notations of forces, stresses, strains, and Hooke’s law in two and three dimensions.
Apply the transformation of stress and strain components under different coordinate systems.
Identify the principal stresses and strains, stress and strain invariants, strain energy, and superposition principle.
Solve two-dimensional problems in Cartesian and polar coordinates using Airy’s stress function method.
Analyze torsion of bars with different cross-sectional shapes using stress function, energy, and numerical methods.
The course will also expose the students to some experimental techniques and analytical tools for solving elasticity problems, such as soap films and Prandtl’s membrane analogy. The course will require the students to apply the concepts and methods learned in class to solve homework assignments and design projects. The course will also prepare the students for more advanced courses in solid mechanics, such as plasticity, fracture mechanics, and finite element analysis. The course is suitable for students who have completed courses in engineering mechanics, mathematics, and physics. The course will be taught through online video lectures.
The topics covered in this course are:
Introduction: Definition and notation for forces and stresses, components of stress and strain, Generalized Hooke’s law, Stress-strain relations in three directions, Plane stress and plane strain, Equations of equilibrium and compatibility in two and three dimensions, Stress components on an oblique plane, Transformation of stress components under change of co-ordinate system.
Principal stresses and principal planes: Stress invariants, Mean and Deviator stress, Strain energy per unit volume, Distortion strain energy per unit volume, Octahedral shear stress, Strain of a line element. Principal strains, Strain invariants, Volume strain, Principle of superposition, reciprocal theorem.
Two dimensional problems in Cartesian co-ordinates: Solution by polynomials, St. Venant’s Principle, Uniqueness of solution, Stress components in terms of Airy’s stress function. Applications to Cantilever, simply supported and fixed beams with simple loading.
Two dimensional problems in Polar co-ordinates: Stress-strain components, Equilibrium equations, Compatibility equations, Applications using Airy’s strain functions in polar co-ordinates for stress distributions symmetric about an axis, Effect of hole on stress distribution in a plate in tension, Stress due to load at a point on a semi-infinite straight boundary, Stresses in a circular disc under diametrical loading.
Torsion: Torsion of various shapes of bars, Stress function method of solution applied to circular and elliptical bars, Torsion of rectangular bars, Solution of Torsional problems by energy method, use of soap films in solving torsion problems, Prandtl’s membrane analogy. Solution of torsion of rectangular bars by (i) Raleigh Ritz method and (ii) Finite difference method.
Who this course is for:
- This course is intended for ME or MTech Structural Engineering students
User Reviews
Rating
Abdul Azeem
Instructor's Courses
Udemy
View courses Udemy- language english
- Training sessions 29
- duration 8:34:43
- Release Date 2023/12/16